Od lat wiadomo, że mózg jako organ jest wyspecjalizowany w rozpoznawaniu i wyszukiwaniu wzorców. Ta właściwość niewątpliwie stanowi ewolucyjną przewagę w świecie zwierząt, między innymi pomaga rozpoznawać drapieżniki, pożywienie, czy inne osobniki swojego gatunku. Ludzie są zdecydowanie mistrzami w tej dziedzinie i dzięki tym umiejętnościom jesteśmy w stanie porozumiewać się za pomocą mowy, czytać, czy przewidywać rzeczy bazując na faktach. Ta umiejętność wpływa również na nasze preferencje, na przykład obiekty symetryczne są z reguły przez większość ludzi uważane za ładniejsze niż ich asymetryczne bądź zdeformowane odpowiedniki.
Jednym z powszechnie uważanych za najestetyczniejszy wzorzec, który można zaobserwować zarówno w naturze jak i sztuce, jest złoty podział, lub inaczej boska proporcja. Jest to taki podział odcinka na dwie części, aby stosunek długości dłuższej do krótszej części był taki sam jak stosunek całego odcinka do dłuższej części. Oznaczany on jest grecką literą φ („fi”). Liczba φ jest liczbą niewymierną, co oznacza że nie da się jej zapisać za pomocą ilorazu dwóch liczb całkowitych, a jej wartość wynosi (1 + √5)/2 lub inaczej około 1,618. Występowanie złotego podziału możemy zaobserwować praktycznie wszędzie, co sprawiło że liczba φ stała się powszechnie rozpoznawalna nie tylko wśród matematyków, ale między innymi i malarzy, muzyków, architektów czy designerów. Złota proporcja zazwyczaj przejawia się za sprawą liczb z ciągu Fibonacciego, czyli takiego ciągu liczb, gdzie pierwszy i drugi wyraz ma wartość 1 (niektóre źródła stanowią że pierwszy wyraz jest równy 0), a każdy następny stanowi sumę dwóch poprzednich, więc pierwsze siedem wyrazów ciągu wygląda następująco: 1, 1, 2, 3, 5, 8, 13… . Co ciekawe proporcje kolejnych par liczb ciągu Fibonacciego zbliżają się do złotej proporcji: 1/2 = 0.5, 2/3 = 0.6(6), 3/5 = 0.6, 5/8 = 0.625 itd. .
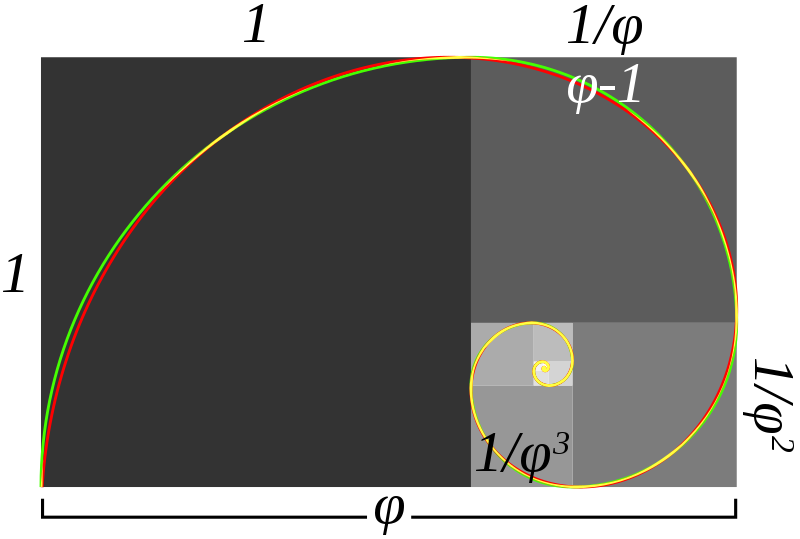
czerwony – złota spirala
żółty – fragmenty pokrywające się
W przyrodzie, wśród roślin, możemy zaobserwować złotą proporcję między innymi za sprawą liczby płatków w kwiatach, które w znaczącej większości przypadków są zgodne z liczbami z ciągu Fibonacciego. Poza tym w wielu roślinach widać spiralne wzory (np. na ananasie, słoneczniku, szyszkach, sukulentach), których liczba również podlega złotej proporcji, np. na owocu ananasa 8 takich linii biegnie w jedną stronę, a 5 lub 13 w przeciwną. Innym flagowym przykładem występowania złotej proporcji w naturze są muszle łodzików i ślimaków, czy rogi baranów, których spirala rażąco przypomina złotą spiralę (spiralę logarytmiczną zależną od φ). Innym przykładem występowania złotej spirali w naturze są huragany które się zgodnie z nią formują, bądź galaktyki spiralne, których spirale są jej przybliżeniem. Istnieje jeszcze wiele innych przykładów, gdzie można w naturze zaobserwować występowanie złotej proporcji, ale poza tym występuje ona również w kulturze w najróżniejszych formach od muzyki (kanon D-Dur Pachelbela) przez architekturę (np. Partenon, piramidy czy katedra Notre-Dame) aż do logo znanych marek (np. Apple, Pepsi, Toyota), a wszystkich miejsc, gdzie można się dopatrzeć tego wzorca nie sposób jest wymienić.

Mimo że ilość miejsc, w których występuje złoty podział jest przytłaczająca, nie należy zapominać o naturze ludzkiego mózgu, który jest wręcz stworzony do wyszukiwania wzorców. Przez co, jeśli zaczniemy szukać jakiejś prawidłowości praktycznie pewne jest to, że ją znajdziemy w takiej bądź innej formie – podobnie jak za sprawą zjawiska pareidoli jesteśmy w stanie zobaczyć znajome wzorce (np. twarze) w przypadkowych miejscach (np. gniazdkach kontaktowych). Należy jednak pamiętać, że nie bez powodu złota proporcja stała się tak popularna i odpowiednie wykorzystanie jej może być korzystne.
Autor: Paweł Olszewski
Linki do źródeł:
https://en.wikipedia.org/wiki/Golden_ratio
https://pl.wikipedia.org/wiki/Z%C5%82oty_podzia%C5%82
https://pl.wikipedia.org/wiki/Ci%C4%85g_Fibonacciego
Dla tych którzy chcą więcej:
https://www.youtube.com/watch?v=1Jj-sJ78O6M
https://www.youtube.com/watch?v=wb7kPaM8cfg





