Wraz z rozwojem komputerów cyfryzacja zawitała na stałe do praktycznie wszystkich sfer naszego życia. Spowodowało to, że wiele branży, takich jak rozrywkowa czy komercyjna, uległo znaczącym przemianom. Technika generowania obrazów komputerowo (ang. Computer Generated Images – CGI) znacząco zredukowała koszty produkcji efektów specjalnych dla wszelkiego rodzaju filmów i reklam, dodatkowo czyniąc je bardziej realistycznymi i spektakularnymi niż to na co pozwalały tradycyjne metody.


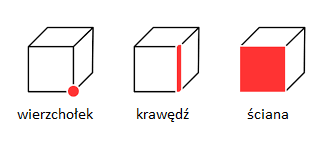
Jednym z najistotniejszych elementów wykorzystywanych podczas generowania grafiki 3D jest model. Stanowi on geometryczną reprezentację przedstawianego obiektu, gdzie większości przypadków składa się z trzech głównych elementów: punktów w przestrzeni trójwymiarowej, krawędzi łączących dokładnie dwa punkty i ścian stworzonych z trzech lub więcej krawędzi (lecz zazwyczaj reprezentują trójkąty i czworokąty, gdyż większa ilość krawędzi może powodować problemy z ich wyświetlaniem).
Z uwagi na fakt, że obecnie wszystkie urządzenia wyświetlają obrazy na dwuwymiarowej płaszczyźnie, aby skorzystać z gotowego trójwymiarowego modelu, potrzebny jest sposób na jego dwuwymiarową wizualizację. Zagadnieniem tym zajmuje się geometria wykreślna. Dowolny model w zależności od potrzeb może być rzutowany na płaszczyznę w sposób równoległy (używany w zastosowaniach inżynierskich) lub perspektywiczny (używany w większości pozostałych zastosowań).
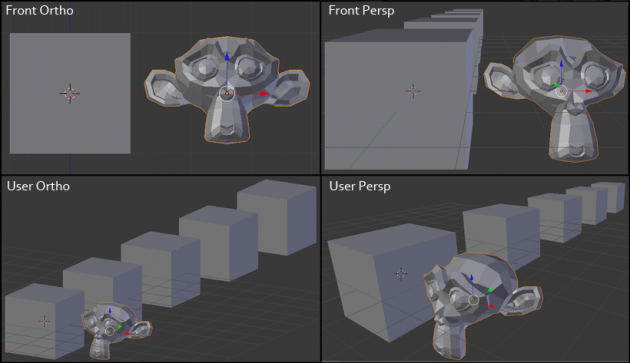
lewo – rzut równoległy; prawo – rzut perspektywiczny
Mając już te dwa elementy jesteśmy w stanie generować prostą grafikę komputerową, lecz warto wzbogacić efekt o dodanie tekstur. Aby to osiągnąć można wybrać jedno z dwóch podejść: teksturowanie z wykorzystaniem obrazów bitmapowych lub funkcji matematycznych. W pierwszym przypadku należy rozwinąć siatkę modelu na dwuwymiarową płaszczyznę, a następnie zapisać na niej obraz, który ma być wyświetlany na odpowiednich ścianach modelu. Drugie podejście pozwala na proceduralną generację tekstur, co znacząco ułatwia proces mapowania, zapewnia zmniejszone zużycie pamięci komputera oraz nieograniczoną rozdzielczość, kosztem zwiększenia czasu potrzebnego do wyliczenia tekstury.


Podstawowym elementem prawie wszystkich tekstur generowanych proceduralnie jest “szumu”. Najistotniejszym algorytmem generowania szumu zdecydowanie jest szum Perlina (ang. Perlin noise). Opracowany w 1983 stanowił rewolucję w dziedzinie proceduralnej generacji ze względu na swój “naturalny” wygląd. Przy jego użyciu (a także innych operacji matematycznych) z łatwością jesteśmy w stanie odwzorować wygląd większości rzeczy występujących naturalnie, takich jak kora drzewa, powierzchnia marmuru czy ogień. Inną wartą wspomnienia strukturą matematyczną wykorzystywaną do tworzenia proceduralnej grafiki jest diagram Voronoi, umożliwiający tworzenie komórkowych struktur lub wszelkiego rodzaju pęknięć.


Z wykorzystaniem tych elementów, odpowiednią ilością czasu i umiejętności można stworzyć komputerową prezentację dowolnego obiektu lub nawet całej sceny. A to jedynie początek tego co oferuje CGI, cała gama zagadnień, od symulacji światła po animacje i efekty specjalne wykorzystujące fizyczne symulacje, pozostaje do odkrycia. Dobrym startem przygody z grafiką komputerową jest darmowy program Blender, pozwalający na to wszystko i wiele więcej, który serdecznie polecam wszystkim zainteresowanym tą dziedziną.
Autor: Paweł Olszewski
Linki do źródeł:
https://en.wikipedia.org/wiki/Perlin_noise
https://en.wikipedia.org/wiki/Gradient_noise
https://en.wikipedia.org/wiki/Procedural_texture
https://pl.wikipedia.org/wiki/Interpolacja_(matematyka)
https://pl.wikipedia.org/wiki/Obrazy_generowane_komputerowo
https://pl.wikipedia.org/wiki/Efekty_specjalne
https://pl.wikipedia.org/wiki/Grafika_3D
https://pl.wikipedia.org/wiki/Teksturowanie
https://en.wikipedia.org/wiki/Voronoi_diagram
Dla tych, którzy chcą więcej:





